Great Triangle Law Of Vector Addition Formula

It can be stated as follows.

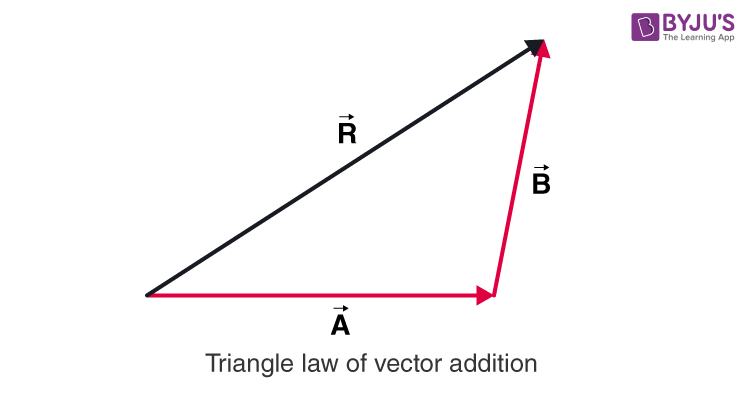
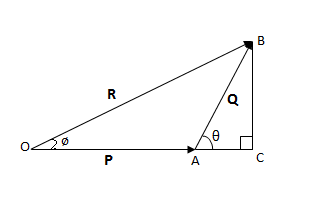
Triangle law of vector addition formula. Represent the vectors and by the two adjacent sides of a triangle taken in the same order. Consider two vectors P and Q acting on a body and represented both in magnitude and direction by sides OA and AB respectively of a triangle OAB. A law which states that if a body is acted upon by two vectors represented by two sides of a triangle taken in order the resultant vector is represented by the third side of the triangle.

Choose any of the two vectors as the first and place the second vectors tail on the head of the first. Let R be the resultant of vectors P and Q. Triangle Law of Addition Two vectors Draw the vectors in pictorial form.

Thus by joining the first vectors tail to the head of the second vector we can obtain the resultant sum vector. Vectors triangle law of in The Oxford Dictionary of Sports Science Medicine. If two sides of a triangle completely represent two vectors both in magnitude and direction taken in same order then the third side taken in opposite order represents the resultant of the two vectors both in magnitude and direction.

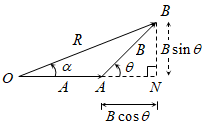
According to the triangle law of vector addition we have from triangle OPR. Triangle Law of Vector Addition The vector addition is dependent when triangles are considered. Then according to parallelogram law of vector addition diagonal OB represents the resultant of P and Q.

Properties of Vector Addition. In Triangle OCB by the triangle law of vector addition b a R 2 From equations 1 and 2. Triangle Law of Vector Addition Statement.

Triangle law of vector addition states that when two vectors are represented as two sides of the triangle with the order of magnitude and direction then the third side of the triangle represents the magnitude and direction of the resultant vector. Triangle Law of Vector Addition. This law is also very similar to the triangle law of vector addition.